Koncepcja przedstawiania wyrazów czy złożonych z nich tekstów za pomocą liczb jest “stara jak świat”. W procesie szyfrowania teksty przekształcane są w ciągi liczb, natomiast podczas deszyfrowania, w sposób wiadomy tylko odbiorcy, dokonuje się operacji odwrotnej. Dzięki temu szyfrowana wiadomość nie dostanie się w niepowołane ręce. Podobno już w starożytnej Grecji stosowano narzędzia szyfrujące: “Wąski pasek pergaminu lub skóry nawijano na laskę, zapisując tekst wzdłuż niej na stykających się brzegach. Będący adresatem posiadacz laski o identycznej grubości mógł szybko odczytać tekst przesłania. W postaci rozwiniętej, z pozbawionymi sensu, rozrzuconymi literami nie miał żadnej wartości dla osoby niepowołanej; zrozumiały był jedynie dla właściwego odbiorcy, który dopasował go do swego wzorca.” (https://pl.wikipedia.org/wiki/Skytale).
Już w 1949 roku amerykański matematyk Warren Weaver sformułował tezę mówiącą, że metodami szyfrowania i deszyfrowania można automatycznie, czyli za pomocą maszyn liczących, przełożyć tekst z jednego języka na inny. Jego wizja spełniła się jednak dopiero po 65 latach, gdy zaczęto publikować pierwsze artykuły o praktycznym wykorzystaniu sieci neuronowych na potrzeby tłumaczenia automatycznego. Dlaczego nie wcześniej? Zapewne z tego powodu, że nie potrafiono wtedy jeszcze reprezentować numerycznie tekstu w taki sposób, aby operacje wykonywane przez sieci neuronowe nie prowadziły do zagubienia sensu wypowiedzi.
Na czym polega trudność w przypadku liczbowej reprezentacji wyrazów?
Wydaje się na pozór, że wyrazy można reprezentować w postaci kolejnych liczb naturalnych, chociażby w kolejności alfabetycznej – przynajmniej w obrębie dokumentu, który jest przetwarzany. Przypuśćmy zatem, że chcemy przetworzyć komputerowo (na przykład w celu przetłumaczenia na inny język czy na potrzeby wyekstrahowania z niego wiedzy) dokument składający się z następujących czterech zdań:
Stolicą Austrii jest Wiedeń.
Stolicą Australii jest Canberra.
Walutą Austrii jest euro.
Walutą Australli jest dolar.
W celu zastosowania metod uczenia maszynowego musimy dokument ten przekształcić do postaci numerycznej. Ułóżmy zatem wszystkie występujące w powyższym tekście wyrazy w porządku alfabetycznym (pomijając kwestię wielkich i małych liter), a następnie przypiszmy poszczególnym wyrazom kolejne liczby naturalne:
australii: 1
austrii: 2
canberra: 3
dolar: 4
auro: 5
jest: 6
stolicą: 7
walutą: 8
wiedeń: 9
Przypuśćmy, że każde z przedstawionych powyżej czterech zdań przedstawimy jako wektor wyrazów wchodzących w jego skład, przy czym każdy wyraz będzie reprezentowany przez odpowiadającą mu liczbę. W takim przypadku dwa pierwsze zdania dokumentu moglibyśmy przedstawić następująco:
Stolicą Austrii jest Wiedeń → {7, 2, 6, 9}
Stolicą Australli jest Canberra → {7, 1, 6, 3}
Chcielibyśmy teraz określić numeryczną reprezentację obu powyższych zdań łącznie. Naturalną operacją wydaje się dodanie obu wektorów:
{7, 2, 6, 9} +
{7, 1, 6, 3} =
{14, 3, 12, 12}
Powstały w ten sposób wektor wynikowy zawiera na trzech miejscach indeksy wyrazów, które nie występują w dokumencie (14 oraz dwukrotnie 12), a na jednym miejscu – wartość 3, czyli liczbę odpowiadającą wyrazowi “canberra”. Okazuje się zatem, że połączenie wyrazów “austrii” oraz “australii” dało nam wyraz “canberra”!
Sieci neuronowe mogą co prawda wykonywać znacznie bardziej złożone operacje na liczbach (oprócz dodawania także mnożenie czy działania z użyciem funkcji), jednak przy zastosowaniu powyższej reprezentacji u podłoża tego typu wyliczeń leżałoby nieuzasadnione założenie, iż np. wyraz “canberra” ma wartość równą sumie wartości wyrazów “australia” oraz “austria”. Nie ma ono niestety sensu semantycznego, dlatego poszukać należy zupełnie innej reprezentacji liczbowej wyrazów.
Co to jest “gorąca jedynka”?
Przyjmijmy, że wszystkie wyrazy mają taką samą wartość – dokładnie 1. Ponownie uszeregujmy teraz zbiór wyrazów zawartych w dokumencie w pewien określony sposób (na przykład w porządku alfabetycznym), reprezentując jednak tym razem każdy z wyrazów w postaci wektora, który na “właściwym” miejscu ma wartość 1, natomiast na wszystkich pozostałych miejscach – wartość zero.
Przykładowo wyraz “australii” (pierwszy w alfabecie) ma jedynkę na pierwszym miejscu:
{1, 0, 0, 0, 0, 0, 0, 0, 0}
podczas gdy wyraz “dolar” (czwarty w alfabecie) ma jedynkę na czwartym miejscu:
{0, 0, 0, 1, 0, 0, 0, 0, 0}
Reprezentację całego zdania otrzymuje się w takim przypadku poprzez wyznaczenie sumy logicznej wektorów wszystkich składających się na to zdanie wyrazów (przy czym suma logiczna dwóch jedynek ma wartość jeden). Na przykład reprezentację zdania:
Stolicą Austrii jest Wiedeń
wyznaczamy następująco:
{0, 0, 0, 0, 0, 0, 1, 0, 0} +
{0, 1, 0, 0, 0, 0, 0, 0, 0} +
{0, 0, 0, 0, 0, 1, 0, 0, 0} +
{0, 0, 0, 0, 0, 0, 0, 0, 1} =
{0, 1, 0, 0, 0, 1, 1, 0, 1}
Analogicznie postępujemy w celu połączenia informacji zawartych w zdaniach. Na przykład łączna reprezentacja zdań: pierwszego (“Stolicą Austrii jest Wiedeń”) i drugiego (“Stolicą Australii jest Canberra”) ma postać:
{1, 1, 1, 0, 0, 1, 1, 0, 1}
Jedynki występują powyżej na miejscach odpowiadających wyrazom, które pojawiły się w pierwszym lub w drugim zdaniu.
Reprezentacja całego dokumentu (wszystkich czterech podanych wcześniej zdań) ma natomiast postać:
{1, 1, 1, 1, 1, 1, 1, 1, 1}
Taki sposób numerycznego reprezentowania wyrazów nosi angielską nazwę “one-hot encoding”, co z przymrużeniem oka przetłumaczyć można jako “kodowanie z gorącą jedynką”. Bardziej adekwatnym polskim odpowiednikiem formalnym powyższej nazwy angielskiej wydaje się jednak tłumaczenie: “kodowanie 1 z n”.
Jak reprezentować liczność występowania?
Oczywistym niedostatkiem “kodowania z gorącą jedynką” jest fakt, że nie bierze ono pod uwagę liczności wystąpienia poszczególnych wyrazów. Choćby w pewnym dokumencie 1000 razy pojawił się wyraz “stolica”, jego waga będzie identyczna jak wyrazu “jarmuż”, o ile tylko drugi z powyższych wyrazów pojawił się w dokumencie choć raz (i to być może przez pomyłkę). System rozpoznawania tematyki takiego dokumentu może w takim przypadku błędnie przyjąć, że tekst dotyczy zdrowej żywności, a nie kwestii polityczno-administracyjnych.
Dlatego właśnie często spotykanym sposobem kodowania jest liczność występowania, zgodnie z którą w wektorze umieszcza liczby wystąpień poszczególnych wyrazów. Reprezentacja naszego przykładowego czterozdaniowego dokumentu ma w przypadku takiego kodowania następującą postać:
{2, 2, 1, 1, 1, 4, 2, 2, 1}
Wyraz “jest”, któremu odpowiada szósty element wektora, występuje w naszym dokumencie 4 razy itd.
Jak reprezentować częstość występowania?
W zestawach złożonych z wielu dokumentów liczność występowania faworyzuje jednak te z wyrazów, które pojawiają się w dłuższych dokumentach (siłą rzeczy ich wystąpień jest po prostu w takich dokumentach więcej). Aby więc “wyrównać szanse” wyrazów pochodzących z krótszych dokumentów, stosuje się reprezentację za pomocą częstości występowania. Zgodnie z nią liczność występowania wyrazu dzielona jest przez liczbę wszystkich wyrazów danego dokumentu. Nasz przykładowy cztero-zdaniowy dokument z niniejszego artykułu jest zgodnie z powyższą metodą reprezentowany w postaci następującego wektora (łącznie wyrazów w dokumencie jest 16, więc każdy z elementów wektora liczności dzielimy przez 16):
{⅛, ⅛, 1/16, 1/16, 1/16,¼, ⅛, ⅛, 1/16}
Polskiemu pojęciu częstość występowania odpowiada angielskie określenie term frequency, oznaczane skrótem TF.
Co oznacza reprezentacja TF-IDF?
Załóżmy, że system komputerowy ma określić tematykę danego tekstu. Wydaje się rozsądne, aby w pierwszej kolejności wziął on pod uwagę wyrazy występujące w tym tekście najczęściej. Czy słusznie? W naszym przykładowym dokumencie najczęściej występuje akurat wyraz “jest”, który niestety niewiele mówi nam o tematyce stosownego tekstu.
Remedium na powyższą bolączkę stanowi reprezentacja TF-IDF. Z jednej strony bierze ona pod uwagę częstość występowania poszczególnych wyrazów w dokumencie (TF), z drugiej jednak strony obniża ona wartość wszechobecnym wyrazom “mało informatywnym” (czyli takim jak: “jest”, “w” czy “z”) poprzez wprowadzenie drugiego czynnika – IDF.
Załóżmy, że oprócz naszego przykładowego dokumentu system analizuje dodatkowo jeszcze trzy inne dokumenty (dysponujemy zatem teraz zestawem czterech dokumentów). Przypuśćmy też, że w każdym z pozostałych trzech dokumentów pojawia się wyraz “jest”, jednak nie występuje w nich żaden inny z wyrazów użytych w naszym przykładowym dokumencie. Wartość IDF (ang. Inverse Document Frequency) danego wyrazu obliczana jest następująco: liczba wszystkich dokumentów zestawu dzielona przez liczbę dokumentów zawierających ten wyraz. Dla wyrazu “jest” IDF wynosi 1 (4/4), natomiast dla pozostałych wyrazów – 4 (4/1).
W przypadku reprezentacji TF-IDF oba czynniki (TF oraz IDF) mnożone są przez siebie, przy czym w odniesieniu do do drugiego z nich stosowana jest najczęściej funkcja logarytmiczna, który to szczegół w tym momencie jednak pominiemy. Reprezentacja naszego przykładowego dokumentu ma więc następującą reprezentację TF-IDF:
{½, ½, ¼, ¼, ¼, ¼, ½, ½, ¼}
I to nam się podoba! Najwyższą wartość mają w przypadku takiej reprezentacji wyrazy: stolicą, prezydentem, Polski, Rosji, które właściwie oddają tematykę analizowanego tekstu.
Co oznacza hipoteza dystrybucyjna?
Reprezentacje: “gorącej jedynki” czy też częstościowe (“patrz Czy wyraz może być liczbą?”) dostarczają informacji na temat zależności pomiędzy wyrazami a dokumentami (informują one, czy dany wyraz pojawia się w dokumencie, jak często w nim występuje i jak częstość ta ma się do częstości jego występowania w innych dokumentach). Nie zawierają one jednak jakichkolwiek informacji na temat znaczenia analizowanych wyrazów.
Czy istnieje zatem jakikolwiek sposób liczbowej reprezentacji znaczenia wyrazów? Z pomocą przychodzi nam w tym miejscu tzw. hipoteza dystrybucyjna, która mówi, że słowa występujące w podobnych kontekstach w obrębie dużych zbiorów danych tekstowych mają prawdopodobnie podobne znaczenie.
Przykładowy dokument może mieć następującą postać:
Stolicą Austrii jest Wiedeń.
Stolicą Australii jest Canberra.
Walutą Austrii jest euro.
Walutą Australii jest dolar.
Taki nieduży dokument w pewnym stopniu potwierdza hipotezę: w podobnych kontekstach pojawiają się bowiem w nim pary wyrazów: <dolar, euro>, <canberra, wiedeń> oraz <stolicą, walutą>. Z powyższych trzech par pierwsze dwie można śmiało uznać za pary wyrazów o podobnym znaczeniu.
Jest dość prawdopodobne, że wyrazy “canberra” oraz “wiedeń” występują w podobnych kontekstach również w innych dokumentach. Natomiast prawdopodobieństwo wystąpienia w podobnych kontekstach wyrazów z ostatniej pary, czyli “stolicą” oraz “walutą”, wydaje się już dużo niższe. Dlatego właśnie w sformułowaniu hipotezy dystrybucyjnej pojawia się pojęcie “dużych zbiorów danych tekstowych”.
Spróbujmy teraz dla podobnych znaczeniowo wyrazów “austrii” i “australii“zbudować ich reprezentację wektorową, wykorzystując w tym celu informacje na temat wyrazów współwystępujących z nimi w tych samych zdaniach w obrębie naszego przykładowego dokumentu.
Poszczególne wyrazy z powyższego dokumentu po uszeregowaniu alfabetycznym prezentują się zaś następująco:
australii: 1
austrii: 2
canberra: 3
dolar: 4
euro: 5
jest: 6
stolicą: 7
walutą: 8
wiedeń: 9
Na podstawie pierwszego ze zdań naszego przykładowego dokumentu zbudujmy teraz wektor dla wyrazu “austrii”, informujący o liczbie wystąpień wyrazów z nim współwystępujących w analizowanym zdaniu (na miejscach odpowiadających wyrazom: “jest”, “stolicą” oraz “wiedeń” pojawią się jedynki, natomiast na pozostałych – zera):
{0, 0, 0, 0, 0, 1, 1, 0, 1}
Zbudujmy analogicznie wektor dla wyrazu “australii” na podstawie drugiego zdania z naszego dokumentu:
{0, 0, 1, 0, 0, 1, 1, 0, 0}
Wektory te są do siebie dość podobne: różnią się na zaledwie dwóch miejscach z dziewięciu.
Podobnie zbudować możemy wektory dla wskazanych powyżej dwóch wyrazów na podstawie zdań trzeciego i czwartego:
{0, 0, 0, 0, 1, 1, 0, 1, 0} (wektor wyrazów współwystępujących dla wyrazu “austrii”)
{0, 0, 0, 1, 0, 1, 0, 1, 0} (wektor wyrazów współwystępujących dla wyrazu wyrazu “australii”)
Możemy teraz zsumować oba wektory opisujące wyraz “austrii”:
{0, 0, 0, 0, 0, 1, 1, 0, 1} +
{0, 0, 0, 0, 1, 1, 0, 1, 0} =
{0, 0, 0, 0, 1, 2, 1, 1, 1}
Możemy również zsumować informacje z obu wektorów opisujących wyraz “australii”:
{0, 0, 1, 0, 0, 1, 1, 0, 0} +
{0, 0, 0, 1, 0, 1, 0, 1, 0} =
{0, 0, 1, 1, 0, 2, 1, 1, 0}
Czy wektory obliczone na podstawie całego dokumentu dla wyrazów “austrii” oraz “australii” są do siebie podobne? Spróbujmy to obliczyć.
Jak wyznaczyć podobieństwo reprezentacji wektorowych?
Czy można jakimś prostym wzorem obliczyć, jak bardzo wektory reprezentujące różne wyrazy są do siebie podobne? Można. Służy do tego miara podobieństwa cosinusowego, której wartości zawierają się między -1 a 1. Podobieństwo wektorów identycznych wynosi 1, natomiast maksymalnie różniących się od siebie wynosi -1.
Odpowiedni wzór przedstawia się następująco:
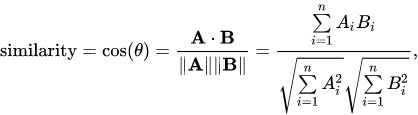
Obliczmy najpierw iloczyn skalarny wektorów reprezentujących odpowiednio wyrazy “austrii” oraz “australii” (licznik powyższego wzoru).
A * B = (0 + 0 + 0 + 0 + 0 + 4 + 1 + 1 + 0) = 6
Obliczmy teraz miary euklidesowe obu wektorów (wchodzące w skład mianownika):
||A|| = sqrt(0 + 0 + 0 + 0 + 1 + 4 + 1 + 1 + 1) = sqrt (8)
||B|| = sqrt(0 + 0+ 1 + 1 + 0 + 4 + 1 + 1 + 0) = sqrt(8)
similarity = 6 / (sqrt(8) * sqrt(8)) = ¾
Maksymalna wartość podobieństwa cosinusowego (dla wektorów identycznych) wynosi 1. Okazuje się zatem, że obliczona miara podobieństwa obu wektorów (¾) jest rzeczywiście dość wysoka.
Czym jest reprezentacja Word2Vec?
Kłopot w przypadku reprezentacji zgodnej z hipotezą dystrybucyjną stanowi sam wymiar wektorów, który jest dokładnie tak duży, jak liczba wyrazów wchodzących w skład zestawu dokumentów (w skrajnym przypadku może ona osiągać wartości rzędu milionów). Wektory o tak dużej liczbie elementów nie nadają się na przykład do obliczeń realizowanych za pomocą sieci neuronowych.
Word2Vec jest reprezentacją wyrazów, u której podstaw leży hipoteza dystrybucyjna, mającą jednak tę dodatkową własność, że wymiar wektora nie przekracza w jej przypadku wartości rzędu kilkuset współrzędnych. Co więcej, wymiar ten nie zależy od wielkości słownika, lecz może być arbitralnie wybrany przez architekta systemu. Reprezentacja Word2Vec oddaje zatem relację podobieństwa wyrazów, a jednocześnie umożliwia realizację zadań z zakresu NLP (takich jak tłumaczenie automatyczne, analiza wydźwięku czy automatyczne generowanie tekstu) przy użyciu sieci neuronowych.
Poniższe zestawienia przedstawiają listy wyrazów, dla których wektory obliczone na podstawie tekstów z Wikipedii są najbardziej podobne do wektorów odpowiadających wyrazom z nagłówków obu kolumn, czyli odpowiednio: “nagoya” (dla lewej kolumny) oraz “coffee” (dla prawej kolumny), co oznacza, że miara podobieństwa osiąga w przypadku tych wyrazów najwyższą wartość.
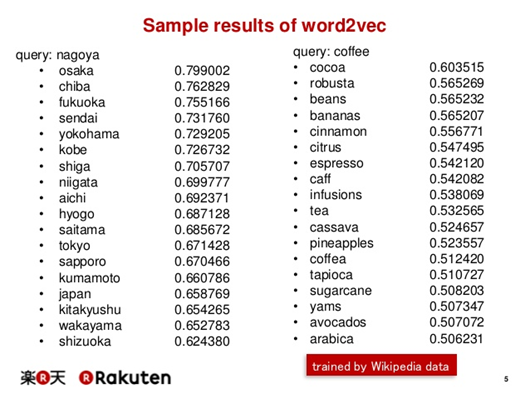
https://www.slideshare.net/rakutentech/recommender-system-with-distributed-representation
Algorytm word2vec
W algorytmie zakładamy, że każdy wyraz reprezentowany jest przez wektor liczbowy o ustalonej długości. Długość ta jest kompromisem pomiędzy możliwościami obliczeniowymi (im krótszy wektor, tym obliczania są mniej wymagające), a dokładnością reprezentacji (im dłuższy wektor, z tym większą szczegółowością może on odzwierciedlać znaczenie wyrazu). W obecnych zastosowaniach najczęściej przyjmuje się długość wektora pomiędzy 300 a 500.
Algorytm dąży do tego, aby wektory wyrazów o podobnym znaczeniu miały wysoką miarę podobieństwa cosinusowego, a wyrazy o znaczeniach odległych miały niską miarę podobieństwa cosinusowego.
Weźmy pod uwagę korpus krótkich przepisów kucharskich.
“Jako się robi marchewkę z groszkiem?”
“Kiedy już zmięknie marchewka, dodajemy groszek”.
“Jak długo powinno się gotować marchewkę?”
“Jak długo gotować młody groszek?”
“W jakiej temperaturze piec pączki?”
“Wyjąć pączki z piekarnika i ostudzić”
“Co łatwiej upiec: faworki czy pączki?”
“Przepis na faworki z piekarnika”
Przyjmijmy, że celem algorytmu jest wyznaczenie takich reprezentacji wektorowych interesujących nas pogrubionych wyrazów, aby wysoką wartość miały podobieństwa cosinusowe między wyrazami z grupy: marchewka, groszek, gotować oraz między wyrazami z grupy pączki, faworki, piekarnika, piec. Nie rozróżniamy form odmienionych wyrazów.
Przyjmijmy, że każdy wyraz reprezentujemy wektorem długości cztery. Wektor dzielimy na dwie części równej długości (w tym wypadku po dwa elementy). Pierwsza część nazwijmy reprezentacją wyrazu i oznaczmy ją literą W, a drugą - reprezentacją kontekstu i oznaczmy ją literą C.
W pierwszym kroku algorytm nadaje losowe wartości wektorom. Załóżmy na przykład, że algorytm wylosował następujące wartości wektorów dla naszego słownika siedmiu wyrazów:
faworki: W[1,1] C[7,7]
groszek: W[2.2], C[6,6]
pączki: W[3,3], C[5,5]
piec: W[4,4], C[4,4]
marchewka: W[5,5], C[3,3]
piekarnik: W[6,6]. C[2,2]
ugotować: W[7.7], C[1,1]
Podobieństwo cosinusowe groszku do pączków wynosi według takich wektorów:
(6 + 6 + 30 + 30) / sqrt(4 + 4 + 36 + 36) * sqrt (9 + 9 + 25 + 25) = 72 / sqrt(80)*sqrt(68) = 0.976
Natomiast podobieństwo groszku do marchewki jest na razie niższe i wynosi:
(10+10+18+18) / (sqrt(80) * sqrt 68) = 0,759
Wybierzmy pierwszy wyraz z korpusu,np. marchewka. Będziemy analizować po kolei wszystkie zdania zawierające ten wyraz. Na podstawie każdego z nich będziemy modyfikować wektor W reprezentujący marchewkę oraz wektory C dla pozostałych wyrazów.
Pierwsze analizowane zdanie to: Jak się robi marchewkę z groszkiem?
Szukamy w tym zdaniu wyrazów ze słownika, znajdując “groszek”. Modyfikujemy reprezentacje wyrazów marchewka i groszek tak, aby wektory się do siebie zbliżyły: na przykład w wyrazie marchewka zmniejszamy o jeden wartości wektora W, a w wyrazie groszek zmniejszamy o jeden wartości wektora C.
groszek: Było: W[2,2], C[6,6]. Jest: W[2, 2], C[5, 5]
marchewka: Było: W[5,5], C[3,3]. Jest W[4,4], C[3,3]
Teraz wybieramy losowo wyraz ze słownika, który w analizowanym zdaniu nie występuje - niech to będzie wyraz faworki (W[1,1] C[7,7]). i “oddalamy” go od wyrazu marchewka.
W tym celu możemy zwiększyć wartości W w wyrazie marchewka, ale trochę byśmy wtedy się wtedy oddalili od wyrazu groszek, więc lepiej zmniejszyć wektor C w wyrazie faworki, otrzymując: nową reprezentację: W[1,1], C[6,6].
Każde kolejne zdanie modyfikuje wartości wektorów. Na przykład w zdaniu 2) marchewka jeszcze bardziej zbliży się do wyrazu groszek, a w zdaniu 3 zbliży się do wyrazu gotować.
Po wyczerpaniu wszystkich zdań zawierających wyraz marchewka będziemy analizować wystąpienia wyrazu groszek. W tym kroku będą się zmieniać wartości wektora W dla groszku i wartości wektora C dla pozostałych wyrazów.
Algorytm, który wykonuje zadanie dopasowania wartości wektorów, to algorytm opadającego gradientu, który znajduje wartości minimum dla funkcji wielu zmiennych. W tym wypadku zmiennymi są wszystkie wartości obu wektorów dla wszystkich wyrazów ze słownika, a minimalizowana funkcja składa się z dwóch składowych:
- zsumowane różnice pomiędzy cosinusami wyrazów sąsiadujących w zdaniach (im mniej, tym lepiej)
- zsumowane różnice pomiędzy cosinusami wyrazów niesąsiadujących (im więcej, tym lepiej).
Ostateczna reprezentacja wektorowa wyrazu wynika z połączenia jego wektorów W oraz C po działaniu algorytmu.
Po co aż tyle liczb?
Można by zadać pytanie, dlaczego po prostu nie nadać wyrazowi jednej wartości liczbowej? Wszak liczb jest nieskończenie wiele.
Wyobraźmy sobie, że chcemy określić podobieństwo między ludźmi. Możemy to uczynić na podstawie porównania tylko jednej cechy (np. wzrostu - zakładając, że ludzie podobnego wzrostu są do siebie podobni). Ale przecież ludzie mogą różnić się również wagą. Osoby różniące się wzrostem jednego centymetra i wagą jednego kilograma są zapewne bardziej podobne do siebie niż osoby o identycznym wzroście różniący się wagą 10 kilogramów. A o podobieństwie decydują przecież jeszcze dziesiątki, jeśli nie setki innych łatwo dostrzegalnych cech. Ludzie wydają nam się podobni, jeśli wysoka jest wartość pewnej funkcji podobieństwa, biorącej pod uwagę wiele zmiennych.
Podsumowanie
Istnieje wiele sposobów reprezentacji wyrazów za pomocą liczb. Obecnie najbardziej popularną z nich jest wektor liczbowy wyznaczany za pomocą metody Word2Vec. Ma on wymiar ustalony przez architekta systemu – mieszczący się najczęściej w przedziale od 300 do 500 współrzędnych. Wektor ten odzwierciedla znaczenie wyrazów w taki sposób, że wyrazom o podobnym znaczeniu odpowiadają wektory, dla których miara podobieństwa ma wysoką wartość.
Autor:
prof. dr hab.
Krzysztof Jassem